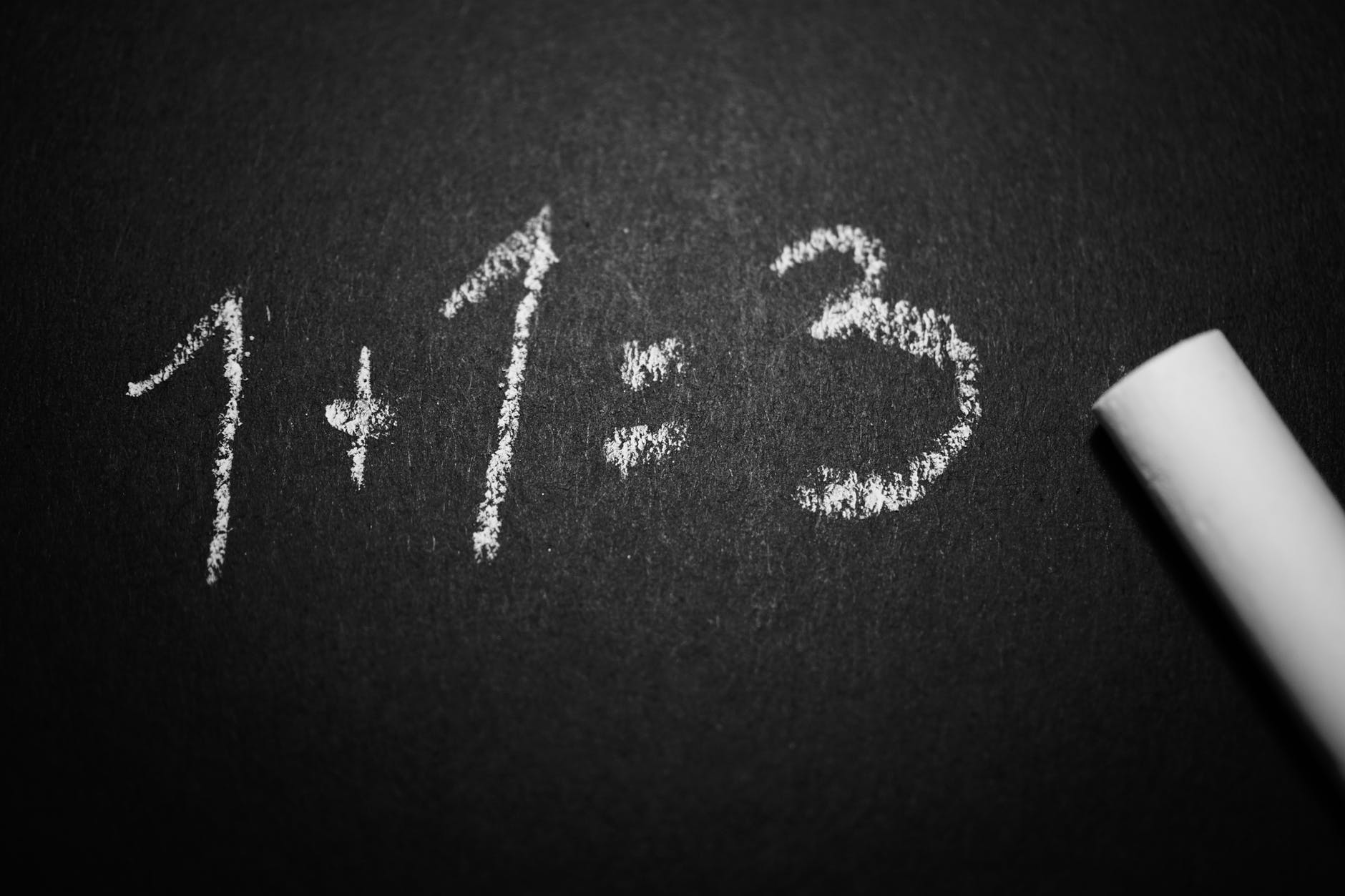Mathematics is an ancient discipline, developed through many cultures and with many different ways of representing numbers and operations. Fortunately, there is a accepted convention that now governs how mathematics is represented around the world and it is through this convention that many mathematicians are able to exchange ideas independent of whether they speak the same (non-mathematical) language. It is not surprising, therefore, that statistics (a branch of mathematics) also has a convention on how statistics are represented.
Statistical Conventions
In the statistics discipline we are typically dealing with one of two groups, the population or the sample. The population we are working with should be denoted by a capital Roman letter (e.g. ) and an individual from that population should be denoted with a lower case Roman letter (e.g.
). When we take a sample from the population, we are getting a set of
‘s out of our population
(i.e each
)